Wir werden hier eine realitätsbezogene, gebrochenrationale Kurvendiskussion durchführen. Wir möchten verstehen, wie man die Probleme und Fragen zur Realität auf die (aus der normalen Kurvendiskussion) bekannten Eigenschaften einer Funktion überträgt.
Reale KD: Gebrochenrat.
Kapiteleintrag
Feuerwerk
1) Die Firma Böller stellt Sylvesterraketen her. Im Zuge neuer Umweltauflagen soll die Rakete "Himmelsfeuer" auf ihren CO2-Ausstoß hin untersucht werden. Die folgende Funktion gibt den Ausstoß (in Milligramm pro Sekunde) einer brennenden Rakete in Abhängigkeit der Zeit (in Sekunden nach dem Start) an.
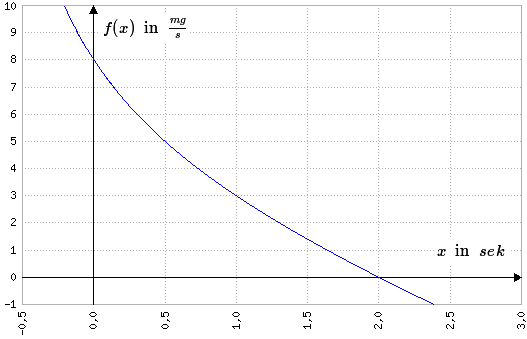
\(f(x)=\frac{-2x^2+8}{x+1}\) a) Wie groß ist die CO2-Ausstoß-Geschwindigkeit eine halbe Sekunde nach dem Start?. b) Zeigen Sie, dass die Rakete nach zwei Sekunden vollständig abgebrannt ist. c) Stimmt es, dass sich die Ausstoßgeschwindigkeit immer langsamer verringert? d) Wieviel Milligramm CO2 wird von einer Rakete der Marke Himmelsfeuer während ihres gesamten Fluges ausgestoßen? 2) Zur Vereinfachung soll der CO2-Ausstoß mit einer linearen Funktion abgeschätzt werden, und zwar derart, dass der Ausstoß zu Beginn (bei \(x=0\)) und zum Ende (bei \(x=2\)) mit dem echten Ausstoß übereinstimmt. a) Geben Sie die zugehörige Funktionsgleichung der linearen Funktion an. b) Die in a) gefundene lineare Funktion darf nur zum Abschätzen des Ausstoßes verwendet werden, wenn sie zu keinem Zeitpunkt um mehr als \(1\frac{mg}{s}\) von der Ursprungsfunktion abweicht. Bestimmen Sie den Zeitpunkt der maximalen Abweichung und geben Sie an, ob die lineare Funktion benutzt werden darf. |
Aufgabe 1a) Ausstoß bei \(x=0{,}5\)?
\(f(x)=\frac{-2x^2+8}{x+1}\) \(f(0,5)=\frac{-2\cdot0,5^2+8}{0,5+1}\) \(=5\;\;(\frac{mg}{s})\) | Da die Funktion selbst die Ausstoßgeschwindigkeit angibt, ist hier einfach der zugehörige y-Wert gesucht. Mit \(f(0,5)=5\) werden eine halbe Sekunde nach dem Start also 5 Milligramm CO2 pro Sekunde abgegeben. |
Aufgabe 1b) Nach zwei Sekunden abgebrannt?
\(f(x)=\frac{-2x^2+8}{x+1}\) \({f}(x)=0\) \(\Rightarrow-2x^2+8=0\) \(\Leftrightarrow{x}=2\vee{x}=-2\) | Die Rakete ist natürlich abgebrannt, wenn sie kein weiteres CO2 mehr ausstößt. Wir suchen also die Nullstelle. Bei gebrochenrationalen Funktionen wird dazu der Zähler Null gesetzt und wir erhalten die Lösungen \(x=2\vee{x}=-2\). Einzig relevant ist die positive Lösung, die Rakete ist also tatsächlich nach zwei Sekunden abgebrannt. |
Aufgabe 1c) Ausstoß verringert sich immer langsamer?
\(f(x)=\frac{-2x^2+8}{x+1}\) \({f}'(x)=\frac{-4x\cdot(x+1)-(-2x^2+8)\cdot1}{(x+1)^2}\) \(\Leftrightarrow{f}'(x)=\frac{-2x^2-4x-8}{(x+1)^2}\) \(\Rightarrow{f}''(x)=\frac{12}{(x+1)^3}\) notw. Bed. f. WST. \(f''(x)=0\) \(\Rightarrow12=0\) \(\Rightarrow\text{keine WST}\) linksgekrümmt? \(\frac{12}{(x+1)^3}\ge0\text{ für }x\ge0\) \(\Rightarrow{f}\text{ ist linksgekrümmt für}x\gt0\) | Dass sich der Ausstoß stets verringert ist bereits aus der Skizze ersichtlich, hier soll aber gezeigt werden, dass sich der Ausstoß immer langsamer verringert. Die Funktion soll also nicht nur stets fallen, sondern auch immer langsamer fallen. Und das schließlich ist bei einer fallenden Funktion dann der Fall, wenn sie linksgekrümmt ist - wir benötigen die Wendestellen. Allerdings hat diese Funktion keine Wendestelle, sie ändert ihr Krümmungsverhalten also nicht. Nun sehen wir an der zweiten Ableitung, dass sie (im betrachteten Intervall) stets positiv ist, die Funktion ist also immer linksgekrümmt - der CO2-Ausstoß verringert sich stets langsamer! |
Aufgabe 1d) Gesamtausstoß während des Fluges?
\(f(x)=\frac{-2x^2+8}{x+1}\) NR.: \((-2x^2+8)\div(x+1)=-2x+2+\frac{6}{x+1}\) \(\Rightarrow{F}(x)=-x^2+2x+6\ln|x+1|\) Berechnung der Fläche \(\int_0^2f(x)dx=F(2)-F(0)\) \(=-2^2+2\cdot2+6\ln|2+1|-(0+0+6\ln|0+1|)\) \(\approx6,59\) | Da die Funktion eine Geschwindigkeit angibt, wird der Bestand durch ein Integral bestimmt, hier das Integral von 0 bis 2. Um eine Stammfunktion zu finden, ist es ratsam, mit Hilfe einer Polynomdivision den ganzrationalen Teil herauszuziehen (wir können diesen ja normal aufleiten). Die Aufleitung des Restglieds ergibt den \(\ln|x+1|\) (beachte, dass die innere Ableitung hier 1 ist. Eigentlich muss man noch durch sie teilen!) Die Fläche selbst sollte dann kein Problem mehr sein - insgesamt werden ca. \(6,59mg\) CO2 abgegeben. |
Aufgabe e) lineare Funktion?
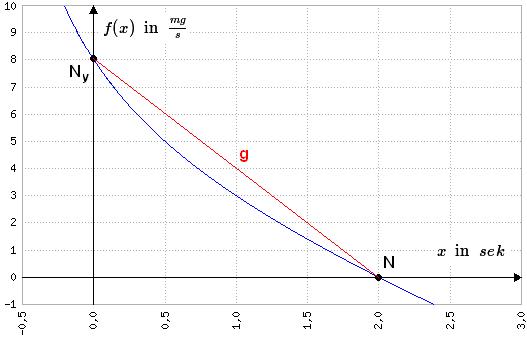
\(P(0|8)\) \(N(2|0)\) \(y=mx+n\) \(m=\frac{0-8}{2-0}=-4\) \(\Rightarrow{y}=-4x+n\) \(8=-4\cdot0+n\Leftrightarrow{n}=8\) \(\Rightarrow{g}(x)=-4x+8\) | Prinzipiell wird hier eine lineare Funktion gesucht, wobei zwei Punkte bekannt sind (P und N). Wir können die Steigung also mit Hilfe des Differenzquotienten berechnen (Steigung zwischen zwei Punkten), in die allgemeine Geradengleichung einsetzen und anschließend \(n\) bestimmen (durch Einsetzen von \(H\) oder \(N\)). Hier hätte man \(n\) übrigens auch ablesen können, denn \(P\) ist ja der y-Achsenabschnitt. | |
| ||
Aufgabe e) Maximale Abweichung?
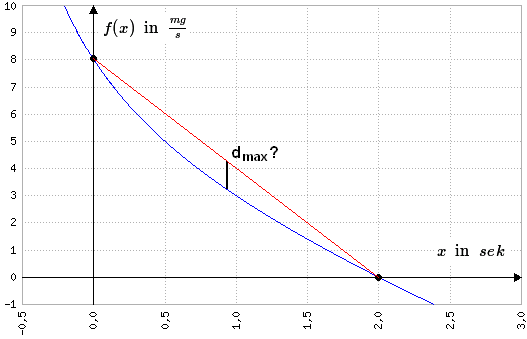
\(d(x)=f(x)-g(x)\) \(d(x)=-2x+2+\frac{6}{x+1}-(-4x+8)\) \(\Leftrightarrow{d}(x)=2x-6+\frac6{x+1}\) Maximaler Abstand? (EST) \(d'(x)=2-\frac6{(x+1)^2}\) \(2-\frac6{(x+1)^2}=0\) \(\Leftrightarrow2(x+1)^2-6=0\) \(\Leftrightarrow(x+1)^2=3\) \(\Leftrightarrow{x}+1=\sqrt3\vee{x}+1=-\sqrt3\) \(\Leftrightarrow{x}\approx0,73\vee{x}\approx2,73\) zugehöriger Abstand? \(d(0,73)=2\cdot0,73-6+\frac6{0,73+1}\) \(\approx0,928\) | Hier liegt eine Extremwertaufgabe vor. Wir bestimmen also zuerst alle Abstände (\(f(x)-g(x)\)), um dann den größtmöglichen zu finden (EST von \(d(x)\)). Hier ist das bei \(x\approx0,73\) der Fall (der andere x-Wert liegt nicht im Intervall), und der zugehörige Abstand beträgt \(0,928\frac{mg}{s}\). Wir dürfen die lineare Funktion also benutzen! | |
| ||
Nützliches
© Christian Wenning
Was ist das KeinPlanPrinzip?
 Grundlagen
Grundlagen Geometrie
Geometrie Terme & Gleichungen
Terme & Gleichungen Funktionen
Funktionen Analysis
Analysis Vektorrechnung
Vektorrechnung Matrizen
Matrizen Stochastik & Statistik
Stochastik & Statistik Sonstiges
Sonstiges