Extrempunkte sind Punkte, die in einer gewissen Umgebung die höchsten (Hochpunkt), bzw. tiefsten (Tiefpunkt) y-Werte annehmen. Man unterscheidet zusätzlich zwischen lokaler und globaler Extremstelle: Während lokale Extremstellen nur höchste oder tiefste Punkte einer bestimmten Umgebung sind, sind globale Extrema die höchsten oder tiefsten Punkte der gesamten Funktion.
- KPIM ›
- Kapitel ›
- Analysis ›
- Kurvendiskussion ›
- Extremstellen
Extremstellen
Kapiteleintrag
Extremstellen
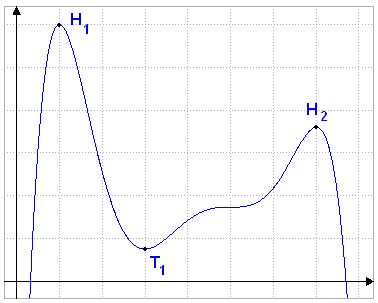
ein lokaler Tiefpunkt \((T_1)\) und ein globaler \((H_1)\) und ein lokaler Hochpunkt \((H_2)\)
Eine besondere Eigenschaft aller Extemstellen ist, dass die Steigung in Extrempunkten \(0\) sein muss. Beispielsweise für einen Hochpunkt muss der Graph erst steigen und dann fallen, im Hochpunkt selbst kann der Graph dann keine Steigung haben. Als Vergleich kannst du dir ein fahrendes Auto vorstellen: Wenn ein Auto erst vor und dann zurück fährt, so muss es zwischendurch gestanden haben.
Diese Eigenschaft läßt sich wunderbar zur Berechnung der Extremstellen ausnutzen, denn Steigungen können wir zuverläßig mit der Ableitung berechnen. Wir müssen also Stellen finden, für die \(f'(x)=0\) ist.
notwendige Bedingung für Extremstellen
\(f'(x_e)=0\)
\(\Rightarrow{x}_e\text{ kann Extremstelle sein}\)
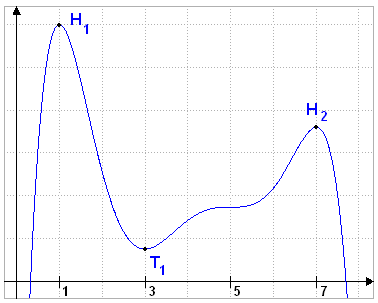
Bei unserer Funktion liefert \(f'(x)=0\) die Lösungen \(x=1\vee{x}=3\vee{x}=5\vee{x}=7\). Betrachtet man aber den Graphen, so fällt auf, dass bei \(x=5\) gar keine Extremstelle ist.
Falsch ist unsere Lösung natürlich auch nicht, denn die Steigung bei \(x=5\) ist wie man sieht \(0\), \(f\) ist dort waagerecht. Wir benötigen also noch ein Kriterium, um solche Stellen - sogenannte Sattelstellen - wieder auszuschließen.
Dazu schauen wir uns einmal die Werte der zweiten Ableitung an besagten Stellen an:
Überprüfung mittels zweiter Ableitung
\(f''(1)=-16\) \(f''(3)=\frac83\) \(f''(5)=0\) \(f''(7)=-8\) | Wir erkennen, dass die zweite Ableitung an unseren Stellen nur bei \(x=5\) Null ist - dort, wo keine Extremstelle ist. Außerdem kann man erkennen, dass die zweite Ableitung bei Hochpunkten negativ \((\)siehe \(f''(1)=-16\) und \(f''(7)=-8)\), und bei Tiefpunkten positiv \((f''(3)=\frac83)\) ist. | |
| ||
Um unsere Extremstellen zu beweisen, müssen wir sie also in die zweite Ableitung einsetzen.
hinreichende Bedingung für Extremstellen
\(f'(x_e)=0\wedge{f}''(x_e)\ne0\)
\(\Rightarrow{x}_e\text {ist eine Extremstelle}\)
Weiter ist \(x_e\)
- Hochpunkt, falls \(f''(x_e)\lt0\)
- Tiefpunkt, falls \(f''(x_e)\gt0\)
Ein Spezialfall liegt vor, wenn die zweite Ableitung auch Null ist: Genaugenommen läßt sich dann über die betrachtete Stelle nämlich keine Aussage treffen, wir benötigen andere Kriterien um die Extremstelle zu überprüfen (z.B. das Vorzeichenwechselkriterium).
In der Schule wird allerdings oft fälschlicherweise einfach behauptet, dass an dieser Stelle dann ein Sattelpunkt vorliegt (so wie das in unserem Beispiel ja auch richtig ist). Besonders schlimm ist der Fehler zwar nicht, da meist tatsächlich ein Sattelpunkt vorliegt, aber in der Mathematik reicht meist natürlich nicht aus!
Am besten fragst du deinen Lehrer, wie er es gern' hätte!
Rezept zum Bestimmen von Extremstellen
➤ Extremstellen werden mit Hilfe der notwendigen und hinreichenden Bedingung bestimmt. Man geht wie folgt vor:
• Bestimme die ersten beiden Ableitungen
• Notw. Bed.: Setzte \(f'(x)=0\) und löse nach \(x\) auf. Du erhälst die Extremstellenkandidaten.
• Überprüfe die Lösungen durch Einsetzen in \(f''\): Ist \(f''(x_e)\lt0\), so liegt ein Hochpunkt vor, bei \(f''(x_e)\gt0\) handelt es sich bei \(x_e\) um einen Tiefpunkt (falls \(f''(x_e)=0\), so liegt wahrscheinlich ein Sattelpunkt vor).
• Ermittle von den bewiesenen Extremstellen noch den zugehörigen y-Wert, falls du den vollständigen Punkt angeben sollst. Das übernimmt natürlich die Ausgangsfunktion, also \(f(x_e)\).
1. Beispiel
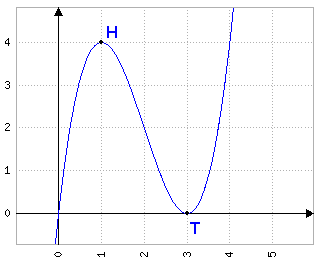
\(f(x)=x^3-6x^2+9x\) Ableitungen \(f'(x)=3x^2-12x+9\) \(f''(x)=6x-12\) Notw. Bed. \(f'(x)=0\) \(3x^2-12x+9=0\) \(\Leftrightarrow{x}=1\vee{x}=3\) Hinr. Bed. \(f'(x)=0\wedge{f}''(x)\ne0\) \(f''(1)=6\cdot1-12\) \(=-6\lt0\Rightarrow{HP}\) bei \(x=1\) \(f''(3)=6\cdot3-12\) \(=6\gt0\Rightarrow{TP}\) bei \(x=3\) y-Werte \(f(1)=1^3-6\cdot1^2+9\cdot1=4\Rightarrow{HP}(1\mid4)\) \(f(3)=3^3-6\cdot3^2+9\cdot3=0\Rightarrow{TP}(3\mid0)\) | Hier dann endlich eine typische Extremstellenberechnung: Wir bestimmen die Ableitungen und setzen die erste gleich Null. Das ergibt mögliche Extremstellen bei \(x=1\vee{x}=3\), welche wir mit \(f''\) überprüfen. Und weil hier tatsächlich zwei Extrempunkte vorliegen, ermitteln wir noch die zugehörigen y-Werte. Hier der Graph:
|
2. Beispiel
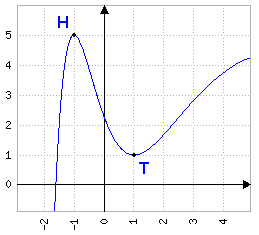
\(f(x)=(-x^2-2x-1)e^{-x+1}+5\) Ableitungen \(f'(x)=(x^2-1)e^{-x+1}\) \(f''(x)=(-x^2+2x+1)e^{-x+1}\) Notw. Bed. \(f'(x)=0\) Hinr. Bed. \(f'(x)=0\wedge{f}''(x)\ne0\) \(f''(-1)=(-(-1)^2+2(-1)+1)e^{-(-1)+1}\) \(\approx-14{,}778\lt0\Rightarrow{HP}\) bei \(x=-1\) \(f''(\;1\;)\;\,\,=(-1^2+2\cdot1+1)e^{-1+1}\) \(=2\gt0\Rightarrow{TP}\) bei \(x=1\) y-Werte \(f(-1)=5\Rightarrow{HP}(-1\mid5)\) \(f(1)=1\Rightarrow{TP}(1\mid1)\) | Hier noch ein Beispiel einer kombinierten e-Funktion. Die Ableitungen werden mit Produktregel gebildet und die erste anschließend gleich Null gesetzt. Die e-Funktion fällt hier direkt weg (sie kann nicht Null werden), die Lösungen des ganzrationalen Teils sind \(x=\pm1\). Bei der Überprüfung ergibt sich ein Hoch- und ein Tiefpunkt, wobei wir anschließend noch die y-Werte mit \(f\) ermitteln. Hier der Graph:
|
Zusatz: Randextrema
Bei Funktionen, die nur für einen bestimmten Bereich gelten (etwa für \(0\le{x}\le12\)), kann es bei der Frage nach dem höchsten, bzw. tiefsten Punkt zu einem Problem kommen. Insbesondere realitätsbezogene Funktionen sind oft auf bestimmte Intervalle eingeschränkt (z.B. das Intervall von gerade, mit \(x\) in Monaten), daher werden wir die Besonderheit an solch einer Funktion erklären. Dazu betrachten wir erneut die aus dem ersten Beispiel bekannte Funktion \(f(x)=x^3-6x^2+9x\), bringen diese nun aber in einen Realitätszusammenhang:
3. Beispiel | Drei Stunden Regen
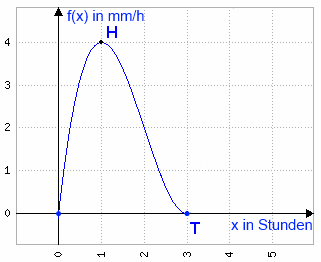
\(f(x)=x^3-6x^2+9x\) Graph
Maximale Regengeschwindigkeit (Intensität)? Lösung: Hochpunkt bei \(H(1|4)\) | Die Funktion soll nun die Regenintensität in \(\frac{mm}{h}\) in Abhängigkeit der seit Regenbeginn vergangenen Zeit in Stunden angeben. Der Regen hört nach drei Stunden wieder auf (die Geschwindigkeit ist dann ja auch null) - wir möchten herausfinden, wann der Regen am stärksten ist. Um das angeben zu können, benötigen wir natürlich den Hochpunkt - denn hier ist die Regengeschwindigkeit maximal. Dieser liegt bei \(H(1|4)\), siehe Bsp. 1, der Regen ist also nach einer Stunde am stärksten (wobei er mit \(4\frac{mm}{h}\) in Mitteleuropa nur als mittelstarker Regenschauer durchgehen würde). |
Soweit, so richtig, die Besonderheit kommt jetzt.
3. Beispiel | Fünf Stunden Regen
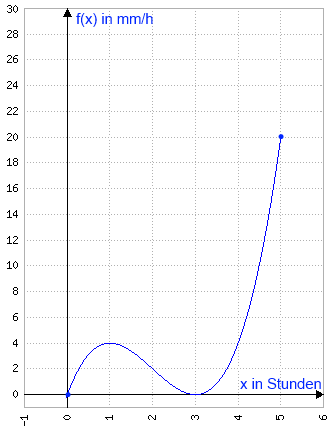
\(f(x)=x^3-6x^2+9x\) Graph
Maximale Regengeschwindigkeit (Intensität)? Lösung: HP bei \(H(1|4)\)??? Höchster Punkt \(f(5)=5^3-6\cdot5^2+9\cdot5=20\) \(\Rightarrow{H}_2(5|20)\) | Die Funktion soll weiterhin die Regenintensität in besagten Einheiten angeben, allerdings betrachten wir den Regenguss nun fünf, statt drei Stunden lang. Wie wir am Graphen direkt erkennen, fängt der Regen nach drei Stunden wieder an, wie beantworten wir jetzt die Frage nach dem Zeitpunkt des stärksten Regen? Die vermeintliche Extremstellenberechnung liefert natürlich weiterhin nur den einen Hochpunkt bei \(H(1|4)\), in der Skizze sehen wir allerdings, dass der Regen nach vier Stunden sogar noch stärker wird! Der höchste Punkt der Funktion - und damit die Antwort auf unsere Frage - liegt am rechten Ende der Funktion, bei \(x=5\). Und wenn wir hier den y-Wert berechnen (die zugehörige Intensität ermitteln), bestätigt sich unsere Beobachtung: Der Regen ist mit \(20\frac{mm}{h}\) sogar fünfmal stärker als im eigentlichen Hochpunkt. |
Bei Funktionen, die nur in einem bestimmten Bereich gelten, kann es also sein, dass die höchsten, bzw. tiefsten Punkte nicht bei den errechneten Extremstellen, sondern am Rand des betrachteten Intervalls liegen. Solch einen Punkt nennt man Randextrema, und wie im Bild zu sehen, kann das sogar der globale Hochpunkt einer Funktion sein!
Wenigstens als Hinweis möchte ich anmerken, warum man die Randextrema nicht gleich bei der normalen Extremstellenberechnung, also bei \(f'(x)=0\) - der notwendigen Bedingung, herausbekommt. Wir hatten eingangs überlegt, dass die notwendige Bedingung Stellen mit Steigung \(0\) suchen muss, da Extremstellen keine Steigung haben. Bei Randextrema muss die Steigung aber nicht Null sein. Betrachte dazu im letzten Beispiel noch einmal den Punkt \(H(5|20)\): Der Graph steigt hier weiter an.
Wir müssen deshalb genaugenommen nach der normalen Extremstellenberechnung immer noch die Randwerte untersuchen.
Rezept zum Bestimmen von globalen Hoch- oder Tiefpunkten unter Berücksichtigung der Randextrema
➤ Bestimme die normalen Extrempunkte auf die übliche Weise.
➤ Bestimme die Funktionswerte an den Funktionsrändern, indem Du die Intervallgrenzen in die Funktion einsetzt.
➤ Entscheide, ob eine normale Extremstelle, oder doch ein Randwert der höchste oder tiefste Punkt ist.
4. Beispiel
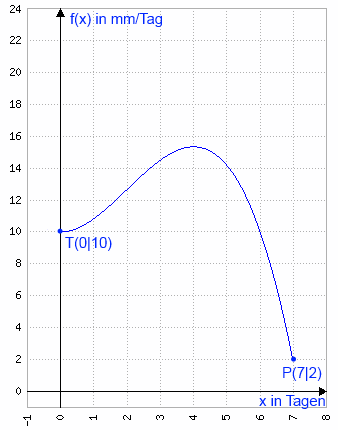
\(f(x)=-\frac16x^3+x^2+10\) Ableitungen \(f'(x)=-\frac12x^2+2x\) \(f''(x)=-x+2\) Extremstellen via n.B. und h.B. \(f'(x)=0\Rightarrow{x}=0\vee{x}=4\) \(f''(0)=2\Rightarrow{TP}\) \(f''(4)=-2\Rightarrow{HP}\) y-Wert des TP \(f(0)=10\Rightarrow{TP}(0|10)\) Randwerte bestimmen \(f(0)=10\), siehe TP \(f(7)=-\frac16\cdot7^3+7^2+10\approx1,833\) Vergleich ESTs und Randwerte \(\Rightarrow{P}(7|1,833)\) ist globaler TP Graph
| Hier soll \(f\) nun die Regenmenge einer Novemberwoche (18. bis 24.11.2013) angeben, es ist \(x\) in Tagen und damit \(0\le{x}\le7\), und \(f(x)\) in \(\frac{mm}{Tag}\). Wir möchten herausfinden, an welchem Wochentag die Niederschlagsmenge minimal war. Zuerst ermitteln wir, ob die Funktion einen normalen Tiefpunkt hat - und finden ihn bei \(T(0|10)\). Da wir den Graphen nicht kennen, halten wir uns an die Abmachung und vergleichen den Tiefpunkt mit den Funktionsrändern, hier \(x=0\) und \(x=7\). Und siehe da: Es fällt auf, dass der tatsächlich tiefste Punkt doch bei \(x=7\) liegt. Insgesamt gab es also am 7. Tag, bzw. am 24. November am wenigsten Niederschlag. Okay, jetzt überprüfen wir das am Graphen... |
Nützliches
© Christian Wenning
Was ist das KeinPlanPrinzip?
 Grundlagen
Grundlagen Geometrie
Geometrie Terme & Gleichungen
Terme & Gleichungen Funktionen
Funktionen Analysis
Analysis Vektorrechnung
Vektorrechnung Matrizen
Matrizen Stochastik & Statistik
Stochastik & Statistik Sonstiges
Sonstiges