Kapiteleintrag
Um den Graphen einer Funktion zeichnen zu können ist es wesentlich zu wissen, wo der Graph herkommt und wo er hinwill. Besser könnte man fragen, was der Graph macht, wenn wir sehr weit nach links gehen (da kommt der Graph her), bzw. wenn wir sehr weit nach rechts gehen. Diese Eigenschaft nennt man das Verhalten für große \(x\) oder das Grenzwertverhalten.
Dieses Kapitel widmet sich der rechnerischen Ermittlung besagter Grenzwerte.
Graph von \(f(x)=\frac15x^3\)
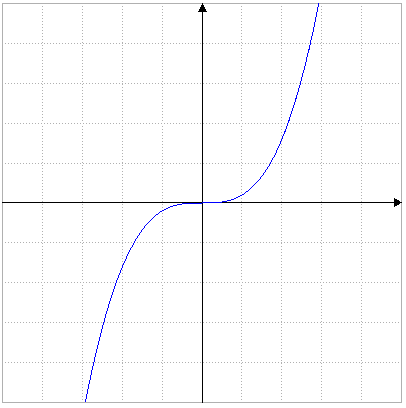
Im Bild läßt sich erkennen, dass der Graph für immer größere \(x\) auch immer größere \(y\) annimmt - der Graph geht nach oben rechts. Analog bekommt man immer kleinere \(y\), je kleiner das eingesetzte \(x\) ist - der Graph verläuft nach unten links.
Wie aber berechnet man diese Ergebnisse?
Nun, die einfachste Möglichkeit, das Grenzwertverhalten einer Funktion zu ermittlen, besteht sicherlich darin, einfach per Hand immer größere positive und negative Zahlen einzusetzen, um zu gucken wogegen die Funktion strebt.
Bestimmen der Grenzwerte per Hand
\(\lim\limits_{x\to\infty}\) \(f(10)=\frac15\cdot10^3=200\) \(f(100)=\frac15\cdot100^3=200{.}000\) \(f(1000)=\frac15\cdot1000^3=200{.}000{.}000\) \(...\) \(\lim\limits_{x\to\infty}f(x)=\infty\)
\(\lim\limits_{x\to-\infty}\) \(f(-10)=\frac15\cdot(-10)^3=-200\) \(f(-100)=\frac15\cdot(-100)^3=-200{.}000\) \(f(-1000)=\frac15\cdot(-1000)^3=-200{.}000{.}000\) \(...\) \(\lim\limits_{x\to-\infty}f(x)=-\infty\) | Bei unserer Funktion \(f(x)=\frac15x^3\) kommen immer größere (positive) y-Werte heraus, je größer positiv das eingesetzte \(x\) ist, analog erhält man immer größere negative Werte, je größer der Wert der eingesetzten negativen Zahl ist. Daraus ergeben sich die angegebenen Grenzwerte (lies: Limes x gegen unendlich f(x) gleich unendlich). Im Bild sind die Grenzwerte durch die Pfeile eingezeichnet: 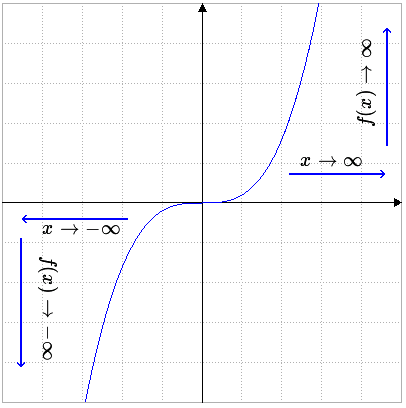
|
Was aber, wenn die Funktion erst viel später ihr Verhalten ändert, wenn sie zum Beispiel bei \(x=1{.}000{.}000\) einen Hochpunkt hat und anschließend doch ins negative Unendliche fällt?
Wir sehen schon, wir benötigen Regeln, um die Limiten mathematisch zu bestimmen!
Diese Regeln werden nun der Reihe nach erklärt. Zuerst berechnen wir noch ein normales Beispiel, um die Vorgehensweise zu erkennen, die anschließenden Beispiele erfordern dann jeweils eine neue Regel.
1. Beispiel
\(f(x)=x^2+4\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((x^2+4)\) \((=\infty^2+4)\) \(=\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \(=\lim\limits_{x\to-\infty}\) \((x^2+4)\) \((=(-\infty)^2+4)\) \(=\infty\) | Für den Grenzwert \(x\to\infty\) überlegt man sich, was passiert, wenn man eine große positive Zahl einsetzt: Hier müssen wir diese große Zahl quadrieren (sie wird noch größer positiv) und anschließend noch \(4\) addieren (das ändert an der großen positiven Zahl fast nichts). Insgesamt wird \(f(x)\) also immer größer (positiv), je größer (positiv) das eingesetzte \(x\) ist. Analog überlegen wir uns, was passiert, wenn wir eine große, negative Zahl einsetzen: Quadriert man diese, so ist sie wieder positiv (und ziemlich groß) und die addierte \(4\) ändert wieder fast nichts: Bspw. ist \((-1000)^2+4=1.000.000+4=1.000.004\). Für \(x\to-\infty\) strebt \(f\) also auch gegen \(+\infty\). |
2. Beispiel
\(f(x)=x^4+5x\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((x^4+5x)\) \((=\infty^4+5\cdot\infty)\) \((=\infty+\infty)\) \(=\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \(=\lim\limits_{x\to-\infty}\) \((x^4+5x)\) \((=(-\infty)^4+5\cdot(-\infty))\) \((=\infty-\infty)\text{ ?}\) | Setzen wir wieder eine große, positive Zahl ein: Diese Zahl hoch \(4\) ist nur noch größer positiv. Hinten müssen wir die große Zahl verfünffachen, sie wird auch dort größer positiv. Anschließend werden beide Ergebnisse addiert, wir erhalten eine riesengroße, positive Zahl. Das Ergebnis ist entsprechend \(+\infty\). Eine große, negative Zahl hoch \(4\) ist wieder positiv (alle Zahlen hoch einen geraden Exponenten sind wieder positiv: Es lösen sich ja immer jeweils zwei Minuszeichen auf), wir erhalten vorne also \(\infty\). Hinten wird die große, negative Zahl verfünffacht, sie bleibt also negativ. Jetzt muss \(\infty-\infty\) berechnet werden, ein unberechenbarer Ausdruck! |
Der Ausdruck \(\infty-\infty\) kann ohne weiteres nicht berechnet werden. Um zu verstehen, dass hier nicht einfach \(0\) herauskommt \((x-x=0)\), musst du dir bewusst machen, dass die beiden Unendlich nicht gleich groß sind!
Dazu bestimmen wir den Grenzwert noch einmal per Hand...
Berechnung per Hand
\(f(x)=x^4+5x\)
\(f(-10)=(-10)^4+5\cdot(-10)=10.000-50=9.950\) \(f(-100)=(-100)^4+5\cdot(-100)=100.000.000-500=99.999.500\) \(f(-1000)=1.000.000.000.000-5000=999.999.995.000\)
\(\Rightarrow\lim\limits_{x\to-\infty}f(x)=+\infty\) | ... und stellen fest, dass das vordere Unendlich viel größer ist, als das Hintere (eine Billionen ist größer als Fünftausend, siehe vorletzte Zeile). Demnach erhalten wir nach dem Subtrahieren immernoch eine sehr große Zahl (\(999.999.995.000\)). \(\infty-\infty\) ist hier also \(+\infty\). |
Wir haben gerade festgestellt, dass die Differenz zweier Unendlich nicht ohne weiteres bestimmbar ist. Man muss wissen, welches Unendlich größer ist, dieses nennt man dann gewichtiger, und es entscheidet über das Ergebnis: Ist das vordere Unendlich gewichtiger, erhält man \(+\infty\), beim hinteren ergibt sich \(-\infty\) und bei gleich großen Unendlich erhält man natürlich \(0\).
Differenz zweier \(\infty\)
\(\infty_1-\infty_2=\infty\text{,}\;\;\text{ falls }\infty_1\text{ gewichtiger}\)
\(\infty_1-\infty_2=-\infty\text{,}\;\;\text{ falls }\infty_2\text{ gewichtiger}\)
\(\infty_1-\infty_2=0\text{,}\;\;\text{ falls gleichgewichtigt}\)
Zum besseren Verständnis kannst du dir auch einfach gewichtigere Zahlen vorstellen: \(1000-10=990\) (also positiv), \(10-1000=-990\) (also negativ) und \(1000-1000=0\).
Übrigens erklärt sich jetzt, warum man einen Ausdruck wie \(\infty^4-5\cdot\infty\) nicht kleinschrittig lösen darf: Nach dem Satz oben ist das Ergebnis der Differenz gleich \(+\infty\), denn \(\infty^4\) ist gewichtiger als \(5\cdot\infty\). Rechnet man den Term aber aus, zu \(\infty^4-5\cdot\infty=\infty-\infty\), so kann man hinten nicht mehr erkennen, welches Unendlich größer ist! Man müsste seine Berechnung stoppen!
Weiter können wir an unserem Beispiel sehen, warum \(\infty^4\) größer ist, als \(5\cdot\infty\), denn bei ersterem müssen wir die große Zahl noch dreimal mit sich selbst mulitiplizieren, hinten nur einmal mit der \(5\) \((1000^3=1.000.000.000\) und \(5\cdot1000=\)nur \(5000)\).
Allgemein ist bei ganzrationalen Funktionen stets das \(x\) mit dem höchsten Exponenten am gewichtigsten!
Grenzwertverhalten von ganzrationalen Funktionen
Bei ganzrationalen Funktionen ist immer das \(x\) mit höchstem Exponenten (samt Vorfaktor) am gewichtigsten.
3. Beispiel
\(f(x)=-2x^3+\frac25x^2-10x+1\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((-2x^3)\) \(=-2\cdot\infty^3\) \(=-\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \(=\lim\limits_{x\to-\infty}\) \((-2x^3)\) \(=-2(-\infty)^3\) \(=\infty\) | Nach gerade gelerntem Satz betrachten wir also nur die \(-2x^3\), denn der komplette Rest hat weniger Gewicht und kann ignoriert werden (veranschauliche dir nochmal unsere per-Hand-Rechnung des letzten Beispiels. Die \(x^4\) wurden so riesig (eine Billion), dass man die \(5x\) hinten (Fünftausend) getrost ignorieren durfte). Okay, für \(x\to\infty\) strebt \(-2x^3\) gegen \(-\infty\) \((\infty^3=\infty\), das mal \(-2\) ist \(-\infty)\) und für \(x\to-\infty\) geht's wieder gegen \(+\infty\), denn \((-\infty)^3=-\infty\), das mal \(-2\) ist wieder positiv. |
4. Beispiel
\(f(x)=-x\cdot{e}^x\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((-x\cdot{e}^x)\) \(=-\infty\cdot{e}^{\infty}\) \(=-\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \(=\lim\limits_{x\to-\infty}\) \((-x\cdot{e}^x)\) \(=-(-\infty)\cdot{e}^{-\infty}\) \((=\infty\cdot0)\text{ ?}\) | Wir berechnen \(-\infty\cdot{e}^{\infty}\) wieder im Kopf: \(e^{\infty}=e\cdot{e}\cdot{e}\cdot...\cdot{e}=\infty\) (da \(e\approx2{,}718\), bedeutet \(e^{\infty}\) ja soviel wie \(2{,}718\cdot2{,}7128\cdot2{,}718\cdot...\cdot2{,}718\) - das ergibt also eine große positive Zahl). Diese mal minus Unendlich und wir erhalten das Ergebnis \(-\infty\). Analog versuchen wir die vorletzte Zeile im Kopf zu lösen: Vorne wird \(-(-\infty)\) positiv, hinten ergibt \(e^{-\infty}\) Null, denn ein negativer Exponent bedeutet nach Potenzgesetzen, dass man den Kehrwert potenzieren soll, also \(e^{-\infty}=\frac{1}{e^{\infty}}\). Der Nenner strebt nun gegen Unendlich (s.o.) und wir erhalten \(\frac{1}{\infty}\). Schließlich strebt ein Bruch, dessen Nenner immer größer wird gegen Null: \(\frac{1}{10}=0{,}1\); \(\frac{1}{100}=0{,}01\); \(\frac{1}{1000}=0{,}001\); ... Wir erhalten also \(\infty\cdot0\), ein ähnliches Problem, wie \(\infty-\infty\)! |
Vorab der Hinweis, dass \(\infty\cdot0\) nicht einfach Null ist \((x\cdot0=0)\), denn unsere Null ist ja nicht genau Null (sie strebt nur dagegen). Betrachten wir dazu wieder die Berechnung der Grenzwerte per Hand:
Berechnung per Hand
\(f(x)=-x\cdot{e}^x\)
\(f(-2)=-(-2)\cdot{e}^{-2}\approx2\cdot0{,}135\approx0{,}280\) \(f(-5)=-(-5)\cdot{e}^{-5}\approx5\cdot0{,}007\approx0{,}035\) \(f(-10)=-(-10)\cdot{e}^{-10}\approx10\cdot0{,}000045\) \(\approx0{,}00045\) \(f(-20)=-(-20)\cdot{e}^{-20}\approx20\cdot0{,}0000000000139\) \(\approx0\) | Wir sehen, dass die e-Funktion viel schneller gegen Null strebt, als das einfache \(x\) vorne gegen Unendlich strebt. Worum es hier geht ist klar, oder? Die Null ist gewichtiger, das Ergebnis des Produkts \(\infty\cdot0\) somit \(0\). |
Übrigens, da wir gerade eine e-Funktion untersuchen: Ist dir aufgefallen, dass wir hier viel kleinere negative Zahlen eingesetzt haben, als in der Beispielaufgabe zu \(\infty-\infty\)? Da hatten wir nämlich \(f(-10)\), \(f(-100)\) und \(f(-1000)\) bestimmt, hier ist \(f(-20)\) das höchste der Gefühle?! Nunja, die e-Funktion ist derart schnell nahe der Null, dass schon beim Exponenten \(-20\) quasi Null herauskommt. Wolle man \(e^{-100}\) angeben, so ergäbe das \(0{,}\text{dreiundvierzigNullen}372\), bei \(e^{-1000}\) sind's 543 Nullen nach dem Komma, bevor eine Zahl kommt!
Die e-Funktion strebt also besonders schnell gegen kleine oder große Werte \((e^{1000}\approx2\cdot10^{434}\), also eine Zahl mit 434 Nullen\()\), wobei "besonders schnell" noch untertrieben ist. Lange Rede wenig Sinn:
Die e-Funktion ist stets gewichtiger, als alle ganzrationalen Funktionen!
Produkt von \(\infty\) und \(0\)
\(\infty\cdot0=\infty\text{, falls }{\infty}\text{ gewichtiger}\)
\(\infty\cdot0=0\text{, falls (die) }{0}\text{ gewichtiger}\)
\(\infty\cdot0=c\text{, falls gleichgewichtigt}\)
Stößt man bei der Grenzwertberechnung auf ein Produkt der Form \(\infty\cdot0\), so entscheidet auch hier das Gewicht über das Ergebnis. Du kannst dir zum Verständnis einfach gewichtigere Zahlen vorstellen: \(1.000\cdot0.1=100\) (große Zahl), \(10\cdot0.0001=0.001\) (nahe Null) und \(10\cdot0.1=1\) (konstant).
Division zweier \(\infty\)
\(\frac{\infty_1}{\infty_2}=\infty\text{, falls }{\infty_1}\text{ gewichtiger}\)
\(\frac{\infty_1}{\infty_2}=0\text{, falls }\infty_2\text{ gewichtiger}\)
\(\frac{\infty_1}{\infty_2}=c\text{, falls gleichgewichtigt}\)
Im Prinzip bedeuten beide Regeln das Gleiche, daher ist die dritte Regel überhaupt direkt mit aufgeführt. Im letzten Beispiel hatten wir zwischendurch ja \(\infty\cdot{e}^{-\infty}\) erhalten - wir haben das umgeformt zu \(\infty\cdot0\), denn \(e^{-\infty}=\frac{1}{e^{\infty}}\to0\). Anders geschrieben wäre \(\infty\cdot{e}^{-\infty}=\infty\cdot\frac{1}{e^{\infty}}=\frac{\infty}{e^{\infty}}=\frac{\infty}{\infty}\) (und mit der gewichtigeren e-Funktion im Nenner wäre das Ergebnis jetzt ebenfalls Null).
Perfekt! Damit kennen wir alle Regeln, die wir zur Bestimmung der Limiten benötigen:
Zusammenfassung Grenzwertverhalten
➤ Das Grenzwertverhalten ermittelt, wo der Graph hingeht \((\lim_{x\to\infty})\) und wo er herkommt \((\lim_{x\to-\infty})\).
➤ Stößt man bei seinen Berechnungen auf \(\infty-\infty\), auf \(\infty\cdot0\) oder auf \(\frac{\infty}{\infty}\), so entscheidet die gewichtigere Funktion über das Ergebnis.
➤ Bei ganzrationalen Funktionen ist stets das \(x\) mit höchstem Exponenten (samt Vorfaktor) am gewichtigsten.
➤ Die e-Funktion ist stets gewichtiger, als alle ganzrationalen Funktionen. Das Grenzwertverhalten dieser Funktion sollte am besten auswendig gewusst werden: \(e^{\infty}\to\infty\) und \(e^{-\infty}\to0\).
So, anders als man jetzt vielleicht denken könnte, ist die Bestimmung der Grenzwerte selbst eigentlich nicht so schwierig. Lediglich die Herleitung der Regeln kommt recht kompliziert daher, in der Praxis ist es machbar! Schaue dir also unbedingt noch die abschließenden Beispiele an.
5. Beispiel
\(f(x)=e^x-(x^2+4x+1)\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((e^x-(x^2+4x+1))\) \((={e}^{\infty}-(\infty^2+4\cdot\infty+1))\) \((=\infty-\infty)\) \(=\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \(=\lim\limits_{x\to-\infty}\) \((e^x-(x^2+4x+1))\) \((={e}^{-\infty}-((-\infty)^2+4\cdot(-\infty)+1))\) \((=0-\infty)\) \(=-\infty\) | Betrachten wir den Grenzwert \(x\to\infty\): Die e-Funktion geht gegen \(\infty\), klar. In der Klammer haben wir eine ganzrationale Funktion, wir betrachten also nur das \(x\) mit höchstem Exponenten, also \(x^2\). Dieses geht für \(x\to\infty\) gegen \(\infty\), wir erhalten insgesamt also eine Ausdruck der Form \(\infty-\infty\). Hier entscheidet das Gewicht, und da die e-Funktion gewichtiger ist, erhalten wir \((+)\) \(\infty\). Dann zu \(x\to-\infty\): Die e-Funktion strebt gegen Null, denn \(e^{-\infty}\to0\). In der Klammer wird wieder nur \(x^2\) betrachtet, bzw \((-\infty)^2\). Dieses wird dank des geraden Exponenten wieder zu \(+\infty\), wir erhalten insgesamt also \(0-\infty\). Ohne auf ein Gewicht zu achten erhalten wir hier \(-\infty\). |
6. Beispiel
\(f(x)=\frac{x^4-x}{x^3+1}\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)\) \(=\lim\limits_{x\to\infty}\) \((\frac{x^4-x}{x^3+1})\) \((=\frac{\infty^4-\infty}{\infty^3+1})\) \((=\frac{\infty}{\infty})\) \(=\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to-\infty}f(x)\) \((=\frac{(-\infty)^4-(-\infty)}{(-\infty)^3+1})\) \((=\frac{\infty}{-\infty})\) \(=-\infty\) | Zuerst zu \(\lim\limits_{x\to\infty}\): Da Zähler und Nenner jeweils ganzrational sind, betrachten wir jeweils nur das \(x\) mit höchstem Exponenten: Im Zähler erhalten wir \(\infty^4=\infty\), im Nenner ist \(\infty^3=\infty\). Da der Zähler gewichtiger ist (hoch 4 ist gewichtiger als hoch 3), erhalten wir insgesamt \(\infty\). Weiter zu \(x\to-\infty\): Da das Prinzip klar ist: Der Zähler strebt gegen \(\infty\), der Nenner gegen \(-\infty\) - letzteres, da \((-\infty)^3=-\infty\). Mit dem gewichtigeren Zähler erhalten wir den Wert \(\infty\), allerdings müssen wir hier \(\frac{+\infty}{-\infty}\) berechnen, das Ergebnis ist also negativ! |
7. Beispiel
\(f(x)=\frac{x^2-1}{e^{x^2-1}}\)
\(\Rightarrow\lim\limits_{x\to\pm\infty}f(x)=0\) | Betrachtet man bei dieser Funktion den Nenner, so strebt \(e^{x^2-1}\) beidseitig gegen \(\infty\) (das \(x^2\) führt stets zu einem positiven Exponenten und \(e^{\infty}\) strebt dann gegen \(\infty\)). Da die gewichtige e-Funktion im Nenner also stets gegen Unendlich strebt, nähert sich die Funktion insgesamt immer der Null an! |
8. Beispiel
\(f(x)=\frac{e^x-e^{-x}}{x+1}\)
\(\lim\limits_{x\to\infty}\) \(\lim\limits_{x\to\infty}f(x)=\frac{e^{\infty}-e^{-\infty}}{\infty+1}\) \((=\frac{\infty}{\infty})\) \(=\infty\)
\(\lim\limits_{x\to-\infty}\) \(\lim\limits_{x\to\infty}f(x)=\frac{e^{-\infty}-e^{-(-\infty)}}{-\infty+1}\) \((=\frac{0-\infty}{-\infty})\) \(=\infty\) | Abschließend noch ein vermeintlich komplizierteres Beispiel: Bei \(x\to\infty\) erhalten wir im Zähler \(e^{\infty}-e^{-\infty}\), das strebt gegen \(\infty-0\), also gegen Unendlich. Der Nenner ist natürlich direkt \(\infty\) und mit der e-Funktion oben erhalten wir insgesamt \(\lim\limits_{x\to\infty}f(x)=\infty\). Für \(x\to-\infty\) erhalten wir im Zähler \(e^{-\infty}-e^{-(-\infty)}\), was gegen \(0-\infty\), also gegen minus Unendlich strebt. Der Nenner ist klar, insgesamt erhalten wir \(\lim\limits_{x\to-\infty}f(x)=\frac{-\infty}{-\infty}=\infty\). |


 Grundlagen
Grundlagen Geometrie
Geometrie Terme & Gleichungen
Terme & Gleichungen Funktionen
Funktionen Analysis
Analysis Vektorrechnung
Vektorrechnung Matrizen
Matrizen Stochastik & Statistik
Stochastik & Statistik Sonstiges
Sonstiges