Baumdiagramm

Kapiteleintrag

Ein Baumdiagramm veranschaulicht mehrstufige Zufallsversuche, also zum Beispiel das mehrmalige Werfen einer Münze oder eines Würfels. Hierbei wird jedes mögliche Ergebnis im Baum dargestellt.

Ein Baumdiagramm zum zweimaligen Münzwurf

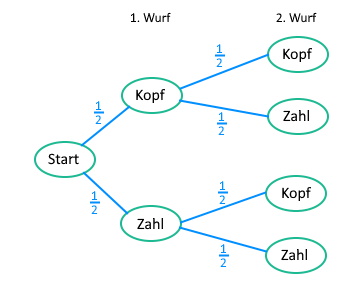Man zeichnet ein Baumdiagramm, indem man zu jeder Stufe des Versuchs alle möglichen Ergebnisse durch einen Ast mitsamt zugehöriger Wahrscheinlichkeit darstellt.

Die erste Stufe unseres zweimaligen Münzwurfs ist der "1. Wurf": Es kann Kopf oder Zahl kommen, also zeichnen wir die beiden Äste ein und notieren an diese jeweils die Wahrscheinlichkeit \(\frac12\).

Beim zweiten Wurf kann nun egal ob wir vorher Kopf oder Zahl geworfen haben wieder jeweils Kopf oder Zahl herauskommen, also zeichnen wir entsprechend jeweils zwei neue Äste mit den Ereignissen und den zugehörigen Wahrscheinlichkeiten \(\frac12\) - fertig ist das Baumdiagramm.

Der fertige Baum gibt nun alle Ergebnisse unseres Versuchs an. Beim zweimaligen Münzwurf kann man die Ereignisse "Kopf Kopf", "Kopf Zahl", "Zahl Kopf" und "Zahl Zahl" erhalten - genau wie man das an unserem Baum sieht.

Wie groß sind jetzt aber die Wahrscheinlichkeiten für diese Ereignisse? Wie wahrscheinlich ist also zum Beispiel das Ergebnis "Zahl Zahl"?

Um das zu berechnen, benötigen wir die 1. Pfadregel.

1. Pfadregel

Um die Wahrscheinlichkeiten der Ergebnisse zu berechnen, werden die zugehörigen Astwahrscheinlichkeiten multipliziert

Das vollständige Baumdiagramm zum zweimaligen Münzwurf

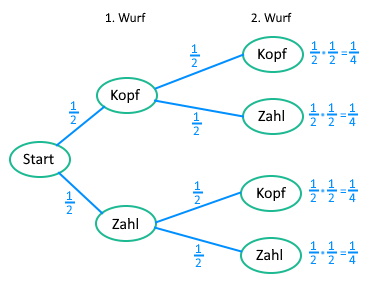Um zum Ereignis "Kopf Kopf" zu gelangen, müssen wir die beiden oberen Äste entlanggehen, also vom Start zum ersten Kopf (Wahrscheinlichkeit \(\frac12\)) und dann weiter zum zweiten Kopf (WSK \(\frac12\)). Die Pfadregel besagt nun, dass wir die zugehörigen Wahrscheinlichkeiten multiplizieren müssen, also erhalten wir für das Ereignis "Kopf Kopf" die Wahrscheinlichkeit \(\frac12\cdot\frac12=\frac14\).

Mit den anderen Ereignissen verfahren wir genauso und können so die Wahrscheinlichkeiten aller Versuchsergebnisse angeben.

Okay, wir können mit Hilfe des Baumdiagramms also die Wahrscheinlichkeiten verschiedener Versuchsergebnisse angeben, so beträgt zum Beispiel die Wahrscheinlichkeit für "zweimal Kopf" \(p(\text{Kopf, Kopf})=\frac14=25\%\) oder für "zweimal Zahl" \(p(\text{Zahl, Zahl})=\frac14=25\%\).

Wie groß aber ist die Wahrscheinlichkeit, beim zweimaligen Münzwurf genau einmal Kopf zu erhalten?

Am Baum sehen wir, dass das Ereignis "genau einmal Kopf" bei zwei verschiedenen Ästen aufkommt: Wir können ja entweder erst Kopf und dann Zahl oder erst Zahl und dann Kopf werfen.

Um die Wahrscheinlichkeiten für solche Ereignisse die mehrere Ast-Möglichkeiten besitzen zu berechnen, benötigen wir die 2. Pfadregel.

2. Pfadregel

Um die Wahrscheinlichkeiten eines Ereignisses zu berechnen, das mehrere Versuchsergebnisse beinhaltet, müssen die zugehörigen Wahrscheinlichkeiten addiert werden.

Alles klar. Die Wahrscheinlichkeit für "Kopf Zahl" beträgt 25%, die Wahrscheinlichkeit für "Zahl Kopf" ebenso - für das Ereignis "genau einmal Kopf" erhalten wir nach 2. Pfadregel also eine Wahrscheinlichkeit von \(p(\text{1 x Kopf})=\frac14+\frac14=\frac12=50\%\).

An dieser Stelle ein kleiner Zusatz, denn man kann sich die Pfadregeln relativ leicht merken, wenn man sich folgenden Zusammenhang verinnerlicht:

Prinzipiell beschreibt die 1. Pfadregel ein "Und-Ereignis", will sagen, um etwa die Wahrscheinlichkeit für das Ereignis "Kopf Kopf" zu bestimmen, muss man im 1. Wurf und im 2. Wurf den Kopf werfen.

Die 2. Pfadregel hingegen beschreibt ein "Oder-Ereignis", so erhält man "genau einmal Kopf", wenn man die Ereignisse "Kopf Zahl" oder "Zahl Kopf" wirft.

Dieser Zusammenhang ("und" bedeutet multiplizieren, "oder" bedeutet addieren) gilt prinzipiell in der gesamten Wahrscheinlichkeitsrechnung und sollte am besten immer im Hinterkopf parat sein. Beispielsweise beträgt die Wahrscheinlichkeit dafür, beim zweimaligen Würfelwurf erst eine 6 und anschließend eine 1 zu würfeln eben \(\frac16\cdot\frac16=\frac1{36}\) - die Wahrscheinlichkeit, in einem Wurf eine 6 oder eine 1 zu erhalten jedoch \(\frac16+\frac16=\frac13\).

Apropos Würfelwurf - zum Abschluss erstellen wir noch schnell ein zweites Baumdiagramm zu einem zweimaligen Würfelwurf.

Baumdiagramm zur Anzahl der 6en beim zweimaligen Würfeln

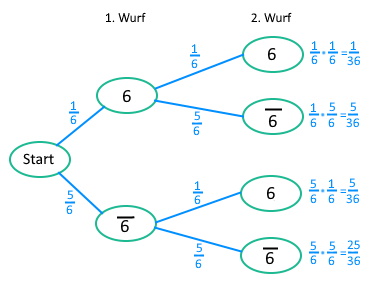Wir steigen direkt beim fertigen Baumdiagramm ein - die 1. Pfadregel wurde also bereits zu allen Ereignissen umgesetzt (für das Ereignis "6 6" müssen wir erst eine 6 werfen und dann noch eine 6 - die WSK hierfür beträgt nach 1. Pfadregel also \(\frac16\cdot\frac16\) usw.).

Mit einem Strich über einem Ereignis kennzeichnet man "Nicht-Ereignisse", \(\overline6\) bedeutet also so viel wie "keine 6 geworfen.

Frage: Wie groß ist die Wahrscheinlichkeit für "mindestens eine 6"?

Antwort: Wir haben bei den Ergebnissen "6 6", " 6 \(\overline6\)" sowie "\(\overline6\) 6" jeweils mindestens eine 6, nach 2. Pfadregel addieren wir diese Wahrscheinlichkeiten also zusammen und erhalten:

\(p(\text{mind. eine 6})=\frac1{36}+\frac5{36}+\frac5{36}=\frac{11}{36}\approx30,6\%\)

Alternativ kann man das auch über die Gegenwahrscheinlichkeit berechnen: Da die Wahrscheinlichkeit für "gar keine 6" \(\frac{25}{36}\) beträgt, erhalten wir mindestens eine 6 zu \(p=1-\frac{25}{36}=\frac{11}{36}\).

Zusammenfassung Baumdiagramm

- man zeichnet ein Baumdiagramm, indem man zu jeder Stufe des Versuchsexperiments jedes Ereignis mit einem Ast und zugehöriger Wahrscheinlichkeit darstellt.

- man erhält die Wahrscheinlichkeit der einzelnen Versuchsergebnisse, indem man nach 1. Pfadregel die zugehörigen Astwahrscheinlichkeiten multipliziert.

- nach 2. Pfadregel berechnet man die Wahrscheinlichkeit von Ereignissen, bei denen mehrere Versuchsergebnisse in Frage kommen, durch Addieren der zugehörigen Wahrscheinlichkeiten.

- Bei vollständigen Bäumen müssen die Wahrscheinlichkeiten der Versuchsergebnisse am Ende des Baumes zusammen 1 bzw. 100% ergeben.