Funktionen können achsensymmetrisch (spiegelbar an der y-Achse) oder punktsymmetrisch (drehbar am Ursprung) sein.
Man ermittelt eine mögliche Symmetrie mit Hilfe der Symmetrietests.
Funktionen können achsensymmetrisch (spiegelbar an der y-Achse) oder punktsymmetrisch (drehbar am Ursprung) sein.
Man ermittelt eine mögliche Symmetrie mit Hilfe der Symmetrietests.
\(f\) ist
- achsensymmetrisch, falls \(f(x)=f(-x)\)
- punktsymmetrisch, falls \(f(x)=-f(-x)\)
Dass z.B. eine achsensymmetrische Funktion \(f(x)=f(-x)\) erfüllen muss, sieht man etwa an der achsensymmetrischen Funktion \(f(x)=x^2\).
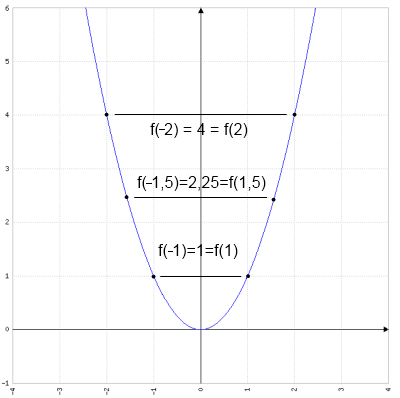
Damit ein Graph nämlich achsensymmetrisch ist, muss jede eingesetzte, positive Zahl das gleiche Ergebnis liefern, wie die zugehörige negative Zahl. Klar, es muss \(f(x)=f(-x)\) sein.
Für den Test auf Punktsymmetrie stelle dir jetzt vor, man würde den linken Teil des Graph (links von der y-Achse) nach unten klappen, also an der x-Achse spiegeln. Das sieht dann so ähnlich aus wie der Graph von \(f(x)=x^3\), jedenfalls erhalten wir eine punktsymmetrische Funktion. Und um an der x-Achse zu spiegeln, muss man eben alle Vorzeichen der y-Werte ändern, gerade (zusätzlich) \(-f(x)\) bestimmen. So gesehen überprüft der Punktsymmetrietest also, ob die Funktion an beiden Achsen gespiegelt werden kann.
\(f(x)=x^2+4\) \(f(-x)=(-x)^2+4\) \(\Leftrightarrow{f}(-x)=x^2+4\text{ }(\text{ }=f(x)\text{ })\) \(\Rightarrow{f}\) ist achsensymmetrisch | Wir testen immer erst auf Achsensymmetrie, bestimmen also \(f(-x)\) und gucken, ob wieder \(f(x)\) herauskommt. Bei dieser Funktion ist das der Fall, \(f\) ist also achsensymmetrisch. |
\(f(x)=2x^3-x\) \(f(-x)=2(-x)^3-(-x)\) \(\Leftrightarrow{f}(-x)=-2x^3+x\text{ }(\text{ }\ne{f}(x)\text{ })\) \(-f(-x)=-\left(-2x^3+x\right)\) \(\Leftrightarrow-f(-x)=2x^3-x\text{ }(\text{ }={f}(x)\text{ })\) \(\Rightarrow{f}\) ist punktsymmetrisch | Hier ist \(f(-x)\) ungleich der Ausgangsfunktion, wir müssen also weitertesten, auf Punktsymmetrie. Da wir jetzt \(-f(-x)\) überprüfen müssen, können wir das Ergebnis des Achsensymmetrietests einfach in eine Minusklammer schreiben, denn \(f(-x)\) kennen wir ja bereits (daher testet man auch erst auf Achsensymmetrie). Diesmal klappt's, \(f\) ist punktsymmetrisch! |
An den beiden Beispielen kann man wunderbar sehen, warum Funktionen punkt- oder achsensymmetrisch sind:
Immer, wenn wir nur gerade Exponenten haben, lösen sich die Minuszeichen von \(-x\) ja wieder auf! Da Minus-mal-Minus Plus ist, eliminiert sich eine gerade Anzahl solcher Zeichen.
Bei ungeraden Exponenten bleibt dementsprechend immer ein Minus übrig, dass wir dann durch \(-f(-x)\) wieder wettmachen!
Eine (vollständig ausmultiplizierte) ganzrationale Funktion ist:
- achsensymmetrisch, falls sie nur gerade Exponenten hat
- punktsymmetrisch, wenn sie nur ungerade Exponenten hat
- keine Symmetrie sonst
Anmerkung: Wenn man so will, hat \(x\) im Falle einer addierten Konstanten den geraden Exponenten \(0\), etwa ist \(f(x)=4\) das gleiche, wie \(f(x)=4x^0\).
Merken musst du dir allerdings nur, dass eine Zahl am Ende immer nur Achsensymmetrie zuläßt!
\(f(x)=x^6+5x^4-\frac13x+2\) \(\Rightarrow{f}\) besitzt keine Symmetrie \(g(x)=x(-x^5+3x)\) \(\Leftrightarrow{g}(x)=-x^6+3x^2\) \(\Rightarrow{g}\) ist achensymmetrisch \(h(x)=(x^2-1)(x+3)-3x^2-3\) \(\Leftrightarrow{h}(x)=(x^3+3x^2-x-3)-3x^2-3\) \(\Leftrightarrow{h}(x)=x^3-x-6\) \(\Rightarrow{h}\) besitzt keine Symmetrie | Bei \(f\) hat \(x\) die Exponenten \(6\), \(4\), \(1\) und \(0\). Wegen der \(1\) besitzt \(f\) keine Symmetrie. \(g\) hat nach dem Ausmultiplizieren nur gerade Exponenten und ist achsensymmetrisch. \(h\) muss auch ausmultipliziert werden, ist wegen der Zahl hinten allerdings nicht punktsymmetrisch! |
Bei nicht-ganzrationalen Funktion müssen wir die normalen Symmetrietests anwenden (zumindest wäre es zu umständlich, für alle Funktionstypen Symmetrieregeln auswendig zu lernen).
\(f(x)=e^{2x+1}\) \(f(-x)=e^{2(-x)+1}\) \(\Leftrightarrow{f}(-x)=e^{-2x+1}\ne{f}(x)\) \(-f(-x)=-\left(e^{-2x+1}\right)\) \(\Leftrightarrow-{f}(-x)=-e^{-2x+1}\ne{f}(x)\) \(\Rightarrow{f}\) besitzt keine Symmetrie | Bei \(f(-x)\) erhalten wir im Exponent der e-Funktion \(-2x+1\), was wir auch durch \(-f(-x)\) nicht mehr eliminieren können. Diese e-Funkiton ist asymmetrisch. |
\(f(x)=x^2e^{-x^2+1}\) \(f(-x)=(-x)^2e^{-(-x)^2+1}\) \(\Leftrightarrow{f}(-x)=x^2e^{-x^2+1}={f}(x)\) \(\Rightarrow{f}\) ist achsensymmetrisch | Der Test auf Achsensymmetrie zeigt, dass \(f(x)=f(-x)\) ist. |
➤ Eine Funktion ist ...
• ... achsensymmetrisch, wenn \(f(x)=f(-x)\)
• ... punktsymmetrisch, wenn \(f(x)=-f(-x)\)
➤ Bei ausmultiplizierten, ganzrationalen Funktionen, kann die Symmetrie an den Exponenten (von \(x\)) abgelesen werden (nur gerade Exponenten: Achsensymmetrie, nur ungerade Exponenten: Punktsymmetrie)
© Christian Wenning
Was ist das KeinPlanPrinzip?
